
腾讯 AI Lab 与瑞士苏黎世联邦理工合作提出基于能量学习的合作博弈新范式,为可解释性等机器学习中的估值问题提供新理论新方法,论文已被 ICLR 2022 接收。
近年来,估值问题在机器学习中变得日益重要。一些典型的估值问题包括用于可解释性的特征归因(feature attribution),用于合作学习的数据估值(data valuation),以及用于集成学习的模型估值(model valuation for ensembles)。开发合理高效的估值算法对于这些应用至关重要。因此,腾讯 AI Lab 与瑞士苏黎世联邦理工合作发表论文《Energy-Based Learning for Cooperative Games, with Applications to Valuation Problems in Machine Learning》,共同提出基于能量学习的合作博弈新范式,为可解释性等机器学习中的估值问题提供新理论新方法。
论文已在 ICLR 2022 发表:

论文链接:https://openreview.net/forum?id=xLfAgCroImw
项目主页:https://valuationgame.github.io/
一、引言:估值问题以及合作博弈的最大熵概率分布
估值问题在各种机器学习应用中变得越来越重要,从特征解释(Lundberg and Lee, 2017)、数据估值(Ghorbani & Zou, 2019)到集成模型估值(Rozemberczki & Sarkar, 2021)。它们通常被表述为合作博弈中的玩家估值问题。一个典型的合作博弈
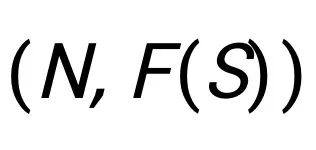
由 n 个玩家 N={1,...,n} 和价值函数(也称为特征函数)
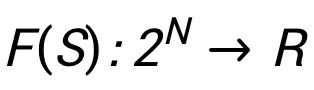
构成,其中价值函数描述任何一个联盟 S 的集体收益。
举个例子, 数据估值 (Ghorbani & Zou, 2019)通常被表述为合作博弈中的玩家估值问题。其中的玩家估值问题目的在于估计每个玩家在此合作博弈中的价值。 如图 1 所示,一个典型的数据估值问题使用 n 个训练样本
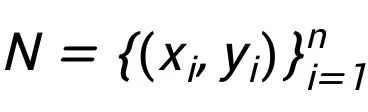
, 进行某种机器学习任务:一个训练样本对应一个玩家,此时价值函数 F(S) 表示使用子集合 S 中的训练样本来训练得到的模型在给定的某个测试数据集上的预测器性能。 使用这种方式,对于一个样本点的估值就转化成了合作博弈中的玩家估值问题。
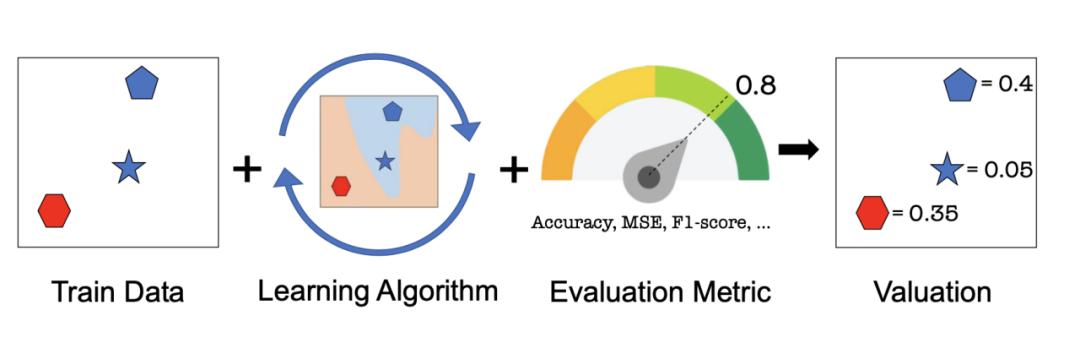
图 1 一个典型的数据估值过程
在本文中,我们研究合作博弈
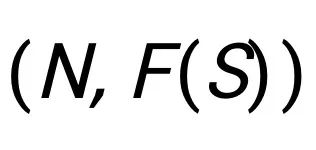
的概率处理方式。这样的处理使得以统一的方式进行学习和推理成为可能,并将产生与经典估值方法的联系。具体来说,我们寻求一组概率分布 p(S),以衡量特定子集合 S 的出现几率。
在所有可能的概率质量函数(probability mass function)中,应该如何构造合适的 p(S)?我们选择具有最大熵
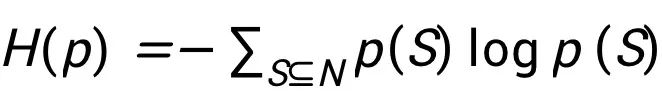
的概率分布。这个设计是有道理的,因为最大化熵会最小化分布中内置的先验信息量,即对未知的东西不做任何假设,选择最 “均匀” 的分布。现在寻求一个合适的概率分布 p(S) 变成了以下的约束优化问题:
假设每个联盟 S 具有收益 F(S),与概率 p(S) 相关联。我们寻求最大化熵 H(p) = -
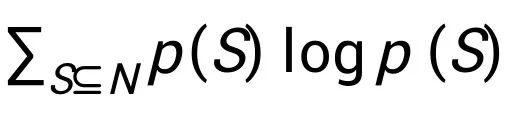
,同时满足约束
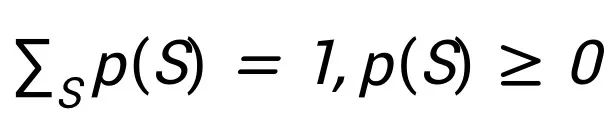
以及
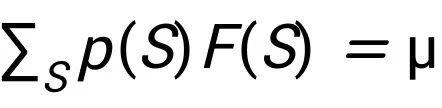
。
求解这个优化问题, 我们得到最大熵分布的形式为:
其中 T>0 是温度参数。这也就是能量模型假设的最大熵分布。
上述基于能量学习的处理有两个好处:i) 在有监督的情况下,它可以通过基于能量学习的有效训练技术来学习价值函数 F(S),例如噪声对比估计 (Gutmann & Hyvärinen, 2010) 和分数匹配(Hyvärinen, 2005)。ii) 可以采用近似推理技术,如变分推理或抽样来解决估值问题。具体来说,它能够执行平均场变分推断,其中推断的代理分布的参数可以用作原则上的玩家估值。
基于能量学习的平均场变分推断的另一个好处在于,我们可以直接建立其与经典估值标准的联系。具体地,通过只进行一步定点迭代(fixed point iteration)来最大化平均场目标,我们恢复了经典的估值标准,例如 Shapley 值 (Shapley, 1953) 和 Banzhaf 值(Penrose, 1946; Banzhaf III, 1964)。这一观察结果也进一步支持了现有方法,因为它们均通过平均场方法解耦玩家之间的相关性。而通过运行多步定点迭代,我们获得了一系列估值轨迹,其中我们将具有最佳可想象解耦误差的估值定义为变分指数。
我们的主要贡献可总结如下:
我们提出了一种理论上合理的基于能量学习的合作博弈处理方式。通过平均场推断,我们为流行的博弈论估值方法提供了统一的视角。这通过解耦的观点为现有标准提供了另一种动机,即通过平均场方法解耦 n 个玩家之间的相关性。
为了得到更好的解耦性能,我们运行多步定点迭代,从而生成一系列变分估值。它们都满足一组博弈论公理,这些公理是合适的估值标准所必备的。我们将具有最佳可想象解耦误差的估值定义为变分指数。
多个实验证明我们提出的变分估值的优异特性,包括更低的解耦误差和更好的估值表现。
二、背景
1. 现有的玩家估值方法
目前的估值方法均使用博弈论中的经典估值方法,比如沙普利值(Shapley value) (Shapley, 1953) 和班扎夫值(Banzhaf value) (Penrose, 1946,Banzhaf III, 1964)。沙普利值给玩家 i 分配的估值为:
其中 |S| 表示联盟 S 中玩家的个数。可以看出,它对 n/2 规模的联盟的权重较小。
班扎夫值给玩家 i 分配的估值为:
它对所有联盟使用统一的权重。
2. 机器学习中的估值问题
目前,大多数类型的估值问题(Lundberg & Lee, 2017 ;Ghorbani & Zou, 2019 ;Sim et al, 2020 ;Rozemberczki & Sarkar, 2021 )使用 Shapley 值作为估值标准。随着过去几十年可解释性机器学习的快速发展(Zeiler & Fergus, 2014;Ribeiro et al, 2016;Lundberg & Lee, 2017;Sundararajan et al, 2017;Petsiuk et al, 2018;Wang et al, 2021a),基于属性的解释旨在为给定黑盒模型 M 的特定数据实例 (x,y) 的特征分配重要性。这里每个特征映射到博弈中的玩家, 而价值函数 F(S)通常是模型的响应,例如当把子集 S 中的特征喂给模型时分类问题的预测概率。一个典型的数据估值问题使用 n 个训练样本N=
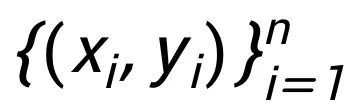
, 进行某种机器学习任务:一个训练样本对应一个玩家,此时价值函数 F(S) 表示使用子集合 S 中的训练样本来训练得到的模型在给定的某个测试数据集上的预测器性能。集成模型评估(Rozemberczki & Sarkar, 2021)测量集合中单个模型的重要性,其中每个预训练模型映射到一个玩家,价值函数测量模型子集的预测性能。
三、方法简介:合作博弈中玩家估值的解耦视角
对于合作博弈的概率分布,方程(1)中所示的概率分布在所有可能分布中实现了最大熵。人们可以很自然地将合作博弈中的玩家估值问题视为解耦问题:博弈中的 n 个玩家可能以非常复杂的方式任意相关。然而,为了给它们中的每一个分配一个单独的重要性值,我们必须解耦它们的交互,这可以被视为简化它们相关性的一种方式。
因此,我们考虑由 x 中的参数控制的代理分布 q(S;x)。q(S;x) 必须简单,因为我们打算解耦 n 个玩家之间的相关性。一个自然的选择是将 q(S;x) 限制为完全可分解的,这导出了对于 p(S) 的平均场近似。q(S;x) 的最简单形式是一个 n 独立的伯努利分布,即
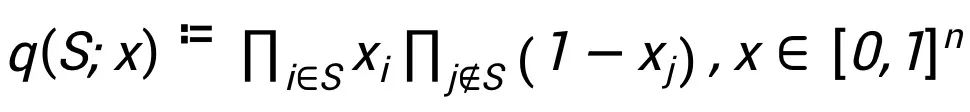
。
接下来我们通过最小化 q(S;x) 和 p(S) 的距离, 来近似原来的最大熵分布 p(S)。
1. 解耦视角的目标函数
接下来我们定义两个分布之间的距离为 Kullback‑Leibler 散度,这样就恢复了平均场方法 (mean field inference)。接下来推导出平均场方法的目标函数。
鉴于式(1)中的最大熵分布,经典的平均场推断方法旨在通过完全分解的乘积分布 q(S;x) 来近似 p(S),通过最小化 q 和 p 之间的 Kullback‑Leibler 散度测量的距离。由于
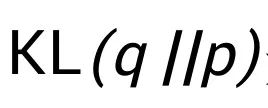
是非负的,我们有:
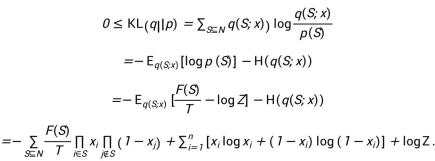
上述式子中,
代表一个概率分布的熵。重新组织上式, 可以得到:
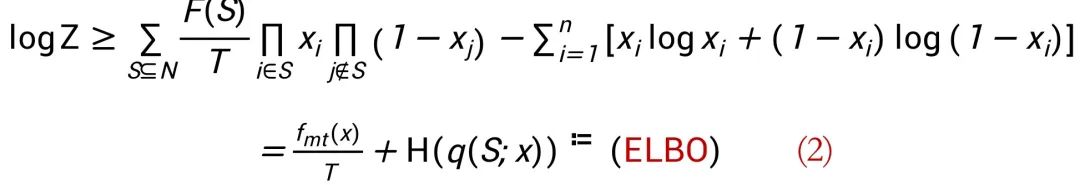
上式中 ELBO 代表 Evidence Lower Bound.
就是此合作博弈的多线性扩展(multilinear extension):
经常上述推导, 我们得出了解耦视角的目标函数, 就是公式 (2) 中的 ELBO 目标函数.
2. 解耦视角下计算变分估值的全梯度平均场算法
为了计算变分估值, 我们首先分析目标函数(2)的均衡条件(Equilibrium condition)。
对于坐标 i,多线性扩展
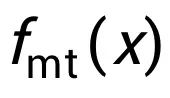
的偏导数是
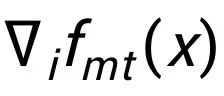
,对于熵项,它的偏导数是
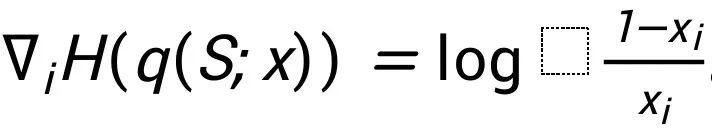
。通过在方程式中将总体的偏导数设为 0, 我们得到均衡条件为:
这种均衡条件意味着无法通过改变分配给任何玩家的价值,以进一步提高整体的解耦性能。它还意味着我们应当使用如下的定点迭代来更新对于每个玩家的估值:
基于上述分析, 我们提出下述的全梯度平均场算法 (Mean Field Inference with Full Gradient), 过程如下:

由此算法产生的估值满足某些博弈论公理。它需要一个初始边际向量
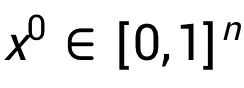
和 迭代次数 K。经过 K 步定点迭代,它返回估计的边际值
。
通过把算法 1 作为子模块, 我们可以定义新的 K 步变分估值方法为:

四、理论分析
我们可以证明, 所提出的 K 步变分估值一方面可以恢复经典的估值算法, 另一方面它满足三个基本的估值公理。
1. 恢复经典的估值算法
令人惊讶的是,可以通过提出的 K 步变分估值恢复经典估值标准。 首先,对于 Banzhaf 值容易推导出:
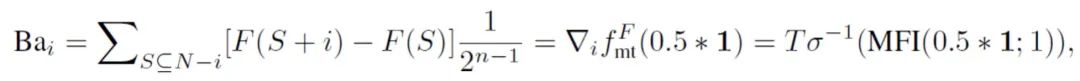
这是在 0.5*1 处初始化的 1 步变分估值。我们还可以通过与多线性扩展的连接来恢复 Shapley 值(Owen, 1972;Grabisch et al, 2000):
其中的积分表示沿单位超立方体的主对角线积分多线性扩展的偏导数。论文附录 D 给出了一个独立的证明。
这些结论为这两个经典估值指数提供了一种新颖、统一的解释:Shapley 值和 Banzhaf 值都可以被视为通过为解耦 ELBO 目标运行一步定点迭代来逼近变分指数。具体来说,对于 Banzhaf 值,它将 x 初始化为,并运行一步定点迭代。对于 Shapley 值,它还执行一步定点迭代。然而,它不是从单个初始点开始,而是通过等式中的线积分对所有可能的初始化值进行平均。
2. 满足三个基本的估值公理
我们的能量学习框架引入了一系列由 T 和运行步数 K 控制的变分估值。我们可以证明所提出的 K 步变分估值满足三个基本估值公理:零玩家(null player)、边缘性 (marginalism) 和对称性 (symmetry)。详细的证明在论文附录 E。

五、实验结果
在实验过程中,我们试图理解以下两点:1)与其他估值方法相比,提出的变分估值方法是否具有更低的解耦误差?2)与经典估值标准相比,我们提出的变分指数能否获得好处?
1. 数据估值实验
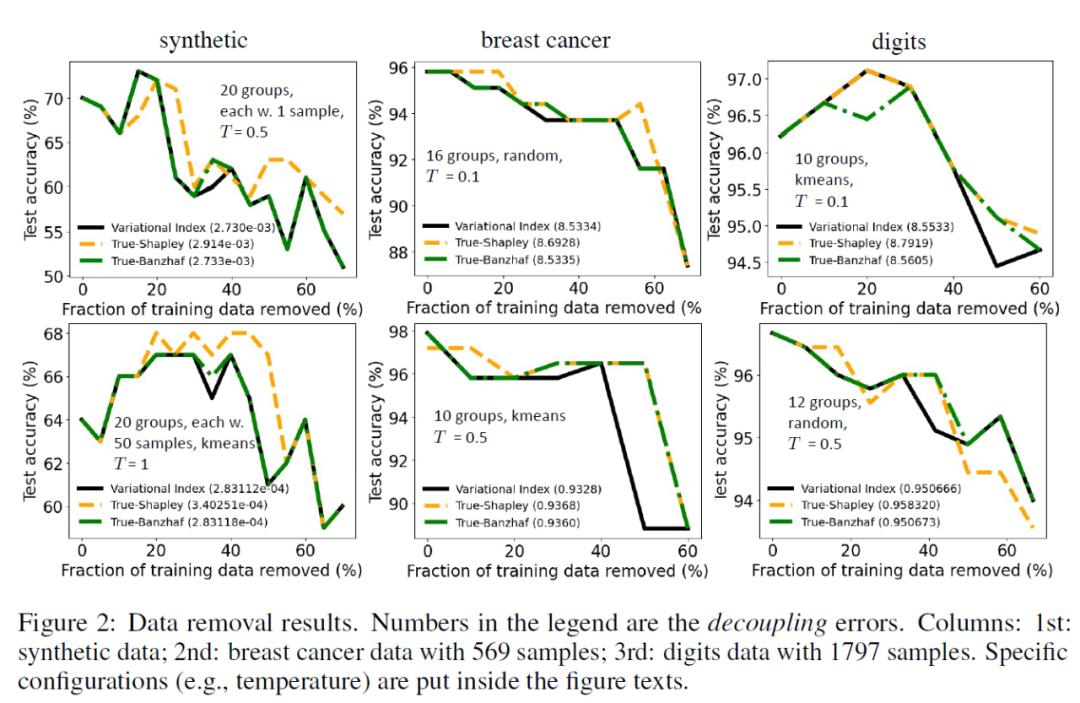
我们按照 Ghorbani & Zou (2019)的设置,复用 https://github.com/amiratag/DataShapley 的代码。我们进行数据去除:根据不同标准返回的估值对训练样本进行排序,然后按顺序去除样本,以检查测试准确率下降了多少。直观地说,最好的估值算法会导致性能下降最快。
图 2 中结果显示:在某些情况下,变分指数达到最快的下降率。它总是达到最低的解耦误差(如每个图中的图例所示)。有时变分指数和 Banzhaf 表现出相似的性能, 我们估计这是因为 Banzhaf 值是变分指数的一步近似值,并且对于所考虑的具体问题,在一步不动点迭代之后,解的排名不会改变。
2. 特征估值 / 归因(feature attribution)实验
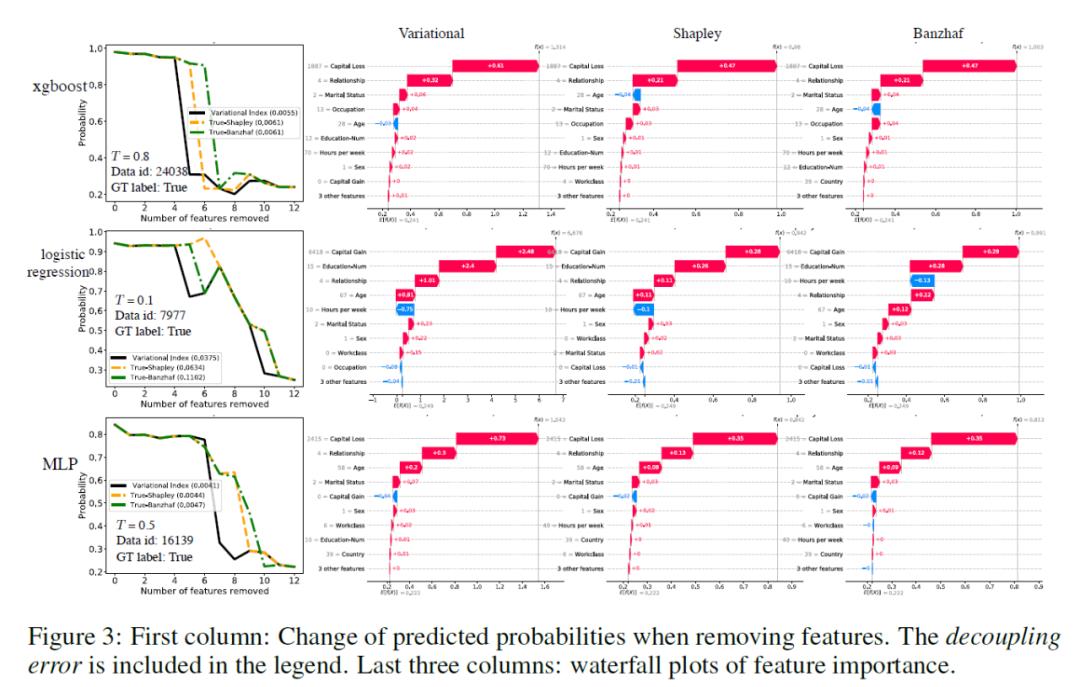
我们沿用 Lundberg & Lee ( 2017)的设置,并使用 MIT 许可证重用 https://github.com/slundberg/shap 的代码。我们在 Adult 数据集 上训练分类器,该数据集根据人口普查数据预测成人的年收入是否超过 5 万美元。
Feature removal results: 该实验遵循与数据去除实验类似的方式:我们根据返回标准定义的顺序逐一去除特征,然后观察预测概率的变化。Figure 3 报告了三种方法的行为。第一行显示来自 xgboost 分类器的结果(准确度:0.893),第二行显示逻辑回归分类器(准确度:0.842),第三行是多层感知器(准确度:0.861)。对于概率下降的结果,变分指数通常引起最快的下降,它总能达到最小的解耦误差,正如其平均场性质所预期的那样。
从瀑布图可以看出这三个标准确实产生了不同的特征排名。以第一行为例:所有标准都将 “Capital Loss” 和“Relationship”作为前两个特征。然而,剩下的特征有不同的排名:变分指数和 Banzhaf 表示 “Marital Status” 应该排在第三位,而 Shapley 则排在第四位。很难说哪个排名是最好的, 因为:1)没有确定特征真实排名的黄金标准;2) 即使存在一些 “完美模型” 的基本事实排名,这里训练的 xgboost 模型可能无法复制它,因为它可能与 “完美模型” 不一致。
六、结论和未来工作
本文介绍了一种基于能量学习的合作博弈方法,以解决机器学习中的若干估值问题。未来在以下方向非常值得去探索: 1)选择温度 T。温度控制公平性水平,因为当时,所有参与者具有同等重要性,当时,参与者具有 0 或 1 重要性。2)给定概率合作博弈的设定,自然可以在玩家之上添加先验,以便编码更多领域知识。3)在基于能量学习的合作博弈框架中探索一群玩家的互动非常有意义,这有助于研究导致多个玩家联盟之间的 “互动” 指数。
部分参考文献
[Ghorbani & Zou, 2019 ] A. Ghorbani and J. Zou. Data shapley: Equitable valuation of data for machine learning. In International Conference on Machine Learning, pages 2242–2251. PMLR, 2019.
[Shapley, 1953] L. S. Shapley. A value for n-person games. Contributions to the Theory of Games, 2(28):307–317, 1953.
[Penrose, 1946] L. S. Penrose. The elementary statistics of majority voting. Journal of the Royal Statistical Society, 109(1):53–57, 1946.
[Banzhaf III, 1964] J. F. Banzhaf III. Weighted voting doesn’t work: A mathematical analysis. Rutgers L. Rev., 19:317, 1964.
[Gutmann and Hyvärinen, 2010] M. Gutmann and A. Hyvärinen. Noise-contrastive estimation: A new estimation principle for
unnormalized statistical models. In Proceedings of the Thirteenth International Conference on
Artificial Intelligence and Statistics, pages 297–304. JMLRWorkshop and Conference Proceedings, 2010.
[Hyvärinen, 2005] A. Hyvärinen. Estimation of non-normalized statistical models by score matching. Journal of
Machine Learning Research, 6(4), 2005.
[Minka, 2001] T. P. Minka. Expectation propagation for approximate bayesian inference. In Proceedings of the Seventeenth conference on Uncertainty in artificial intelligence, pages 362–369, 2001.© THE END